外观
拆分
约 1512 字大约 5 分钟
2025-12-26
对于一门语言的掌握程度怎么样, 可以有两个角度来衡量: 读和写.
不仅要求自己能解决问题, 还要看懂别人的解决方案. 代码是这样, 正则表达式也是这样.
正则这门语言跟其他语言有一点不同, 它通常就是一大堆字符, 而没有所谓语句的概念.
如何能正确地把一大串正则拆分成一块一块的, 成为了破解天书的关键.
结构和操作符
编程语言一般都有操作符. 只要有操作符, 就会出现一个问题. 当一大堆操作在一起时, 先操作谁, 又后操作谁呢? 为了不产生歧义, 就需要语言本身定义好操作顺序, 即所谓的优先级.
而在正则表达式中, 操作符都体现在结构中, 即由特殊字符和普通字符所代表的一个个特殊整体.
具体含义简要回顾如下(如懂, 可以略去不看):
字面量, 匹配一个具体字符, 包括不用转义的和需要转义的. 比如a匹配字符a, 又比如\n匹配换行符, 又比如\.匹配小数点.
字符组, 匹配一个字符, 可以是多种可能之一, 比如[0-9], 表示匹配一个数字. 也有\d的简写形式. 另外还有反义字符组, 表示可以是除了特定字符之外任何一个字符, 比如[^0-9], 表示一个非数字字符, 也有\D的简写形式.
量词, 表示一个字符连续出现, 比如a{1,3}表示“a”字符连续出现3次. 另外还有常见的简写形式, 比如a+表示“a”字符连续出现至少一次.
锚点, 匹配一个位置, 而不是字符. 比如^匹配字符串的开头, 又比如\b匹配单词边界, 又比如(?=\d)表示数字前面的位置.
分组, 用括号表示一个整体, 比如(ab)+, 表示ab两个字符连续出现多次, 也可以使用非捕获分组(?:ab)+.
分支, 多个子表达式多选一, 比如abc|bcd, 表达式匹配abc或者bcd字符子串.
反向引用, 比如\2, 表示引用第2个分组.
其中涉及到的操作符有:
- 转义符:
\. - 括号和方括号:
(...),(?:...),(?=...),(?!...),[...]. - 量词限定符:
{m},{m, n},{m, },?,*,+. - 位置和序列:
^,$,\元字符,一般字符. - 管道符(竖杠):
|.
上面操作符的优先级从上至下, 由高到低.
这里, 我们来分析一个正则:
/ab?(c|de*)+|fg/.
- 由于括号的存在, 所以,
(c|de*)是一个整体结构. - 在
(c|de*)中, 注意其中的量词*, 因此e*是一个整体结构. - 又因为分支结构
|优先级最低, 因此c是一个整体, 而de*是另一个整体. - 同理, 整个正则分成了
a,b?,(...)+,f,g.而由于分支的原因, 又可以分成ab?(c|de*)+和fg这两部分.
希望你没被我绕晕, 上面的分析可用其可视化形式描述如下:
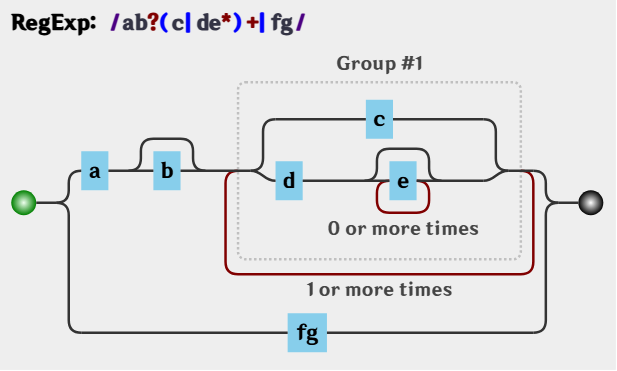
注意要点
关于结构和操作符, 还是有几点需要强调:
匹配字符串整体问题
因为是要匹配整个字符串, 我们经常会在正则前后中加上锚字符^和$.
比如要匹配目标字符串abc或者bcd时, 如果一不小心, 就会写成/^abc|bcd$/.
而位置字符和字符序列优先级要比竖杠高, 故其匹配的结构是:
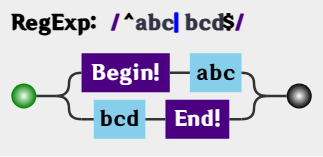
应该修改成:
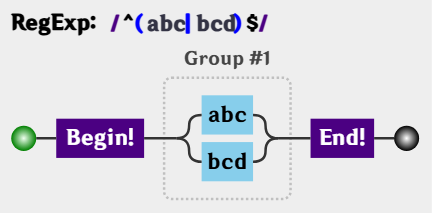
量词连缀问题
假设, 要匹配这样的字符串:
- 每个字符为a, b, c任选其一.
- 字符串的长度是3的倍数.
此时正则不能想当然地写成/^[abc]{3}+$/, 这样会报错, 说+前面没什么可重复的:
此时要修改成:

元字符转义问题
所谓元字符, 就是正则中有特殊含义的字符.
所有结构里, 用到的元字符总结如下:
^, $, ., *, +, ?, |, \, /, (, ), [, ], {, }, =, !, :, -, , .
当匹配上面的字符本身时,可以一律转义:
/\^\$\.\*\+\?\|\\\/\[\]\{\}\=\!\:\-\,/.
其中string中的\字符也要转义的.
另外, 在string中, 也可以把每个字符转义, 当然, 转义后的结果仍是本身.
\^\$\.\*\+\?\|\\\/\[\]\{\}\=\!\:\-\,.
现在的问题是, 是不是每个字符都需要转义呢? 否, 看情况.
字符组中的元字符
跟字符组相关的元字符有[], ^, -.因此在会引起歧义的地方进行转义.例如开头的^必须转义, 不然会把整个字符组, 看成反义字符组.
/[\^$.*+?|\\/\[\]{}=!:\-,]/.
匹配[abc]和{3,5}
我们知道[abc], 是个字符组.如果要匹配字符串[abc]时, 该怎么办?
可以写成/\[abc\]/, 也可以写成/\[abc]/, 测试如下:
/\[abc]/.
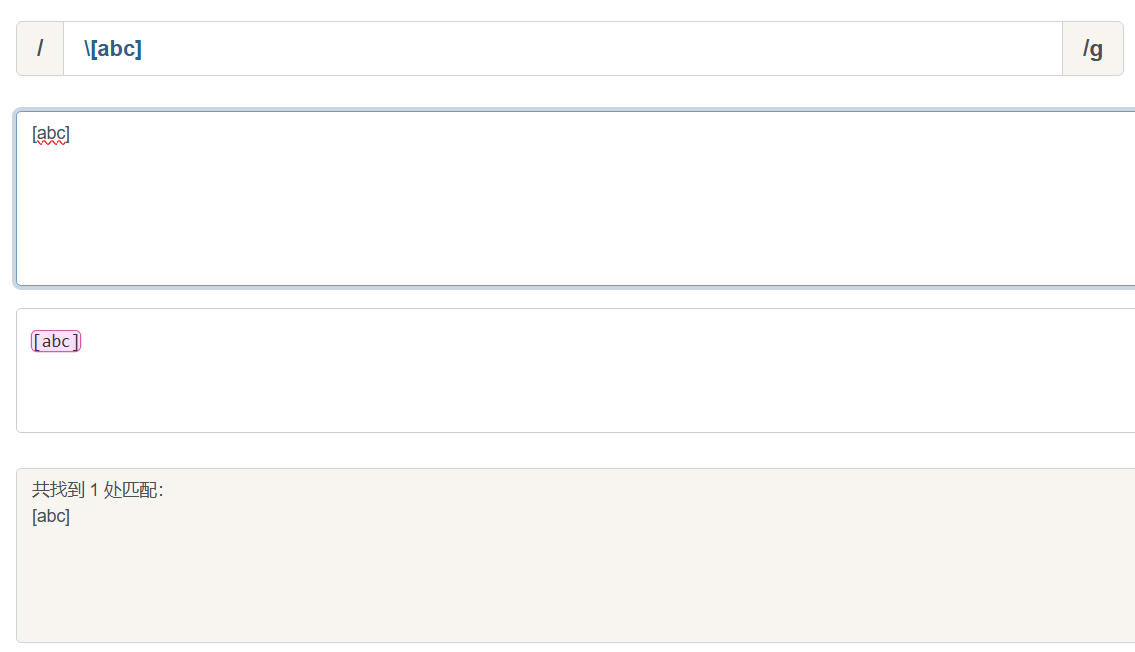
只需要在第一个方括号转义即可, 因为后面的方括号构不成字符组, 正则不会引发歧义, 自然不需要转义.
同理, 要匹配字符串{3,5}, 只需要把正则写成/\{3,5}/即可.
另外, 我们知道量词有简写形式{m,}, 却没有{,n}的情况.
虽然后者不构成量词的形式, 但此时并不会报错.
当然, 匹配的字符串也是{,n}, 测试如下:
/{,3}/.
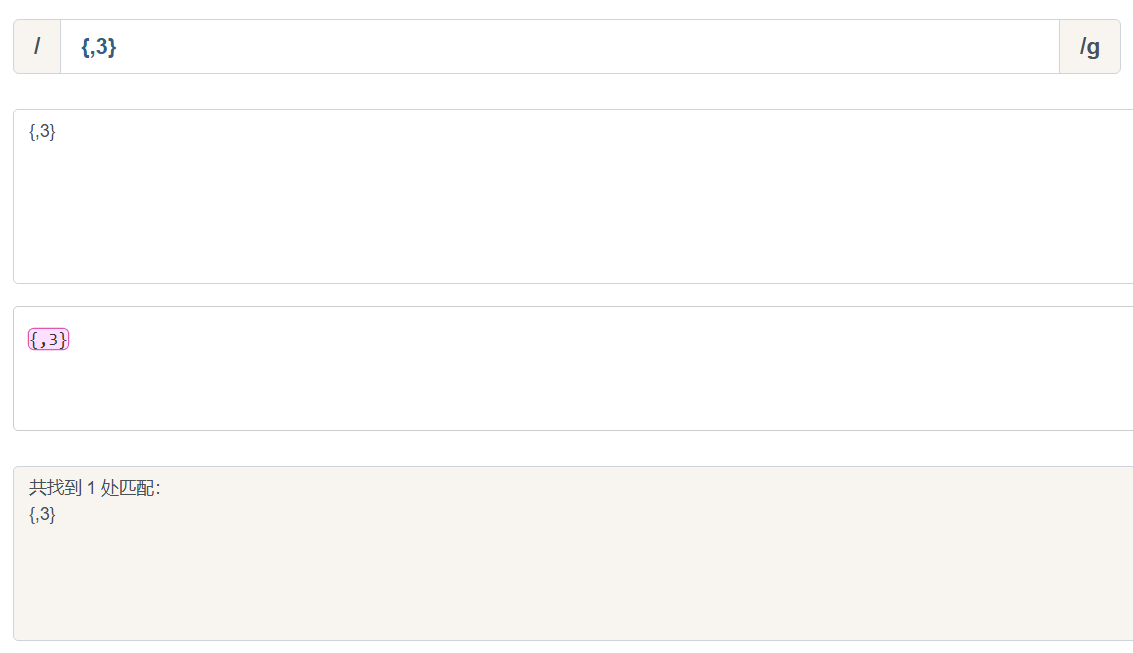
其余情况
比如=, !, :, -, ,等符号, 只要不在特殊结构中, 也不需要转义.
但是, 括号需要前后都转义的, 如/\(123\)/.
至于剩下的^, $, ., *, +, ?, |, \, /等字符, 只要不在字符组内, 都需要转义的.
版权所有
版权归属:Erhai-lake
